基于有限元数值计算的爆破震动强度分析
发布时间:2013-07-31 15:52:00 阅读次数:次
刘红岩 1 ,刘国振 2 ,杨 军 2 ,陈鹏万 2
(1. 中国科学院工程地质力学重点实验室,北京 100029;2. 北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
摘 要:爆破震动强度的预测一直是爆破震动危害控制的前提和基础,也是其研究的一个重要课题。基于有限元数值模拟方 法的基础上对反映爆破震动强度的重要指标——质点振动速度的计算方法进行了探讨,并对空气和水两种不同间隔装药结构 下的震动强度计算结果进行了对比分析。数值模拟结果表明,在爆心距不太大的情况下,计算结果与实测结果吻合较好,研 究结果对爆破设计与施工有一定的指导意义。(1. 中国科学院工程地质力学重点实验室,北京 100029;2. 北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
关 键 词:数值模拟;震动强度;预测;间隔装药
1 引 言
在爆破工程尤其是大型的岩土爆破工程施工 中,爆破震动的预防与控制在爆破施工与设计中占 有至关重要的作用,特别是在爆破环境比较复杂的 情况下,爆破震动的控制显得尤为重要。在目前的 爆破震动控制中,最常用的方法是在已测试出的爆 破震动数据基础上,根据萨道夫斯基公式或模糊控 制理论如神经网络技术等[1~3],得到爆破震动的传 播规律,进而可以对以后的爆破工程起到很好地指 导作用。这种方法在爆破震动的预测及控制中起到 了非常重要的作用,但是这种方法也有一个明显的 缺点就是必须要有大量的震动测试数值为基础,而 在震动测试数据的获得并不是很容易的情况下,这 种方法就显得无能为力了,所以很有必要寻找一种 在事先没有震动测试数据的基础上,能够对爆破震 动强度进行预测的方法,进而对爆破设计与施工起 到指导作用。
本文即提出一种采用数值模拟技术对爆破震动 强度进行估计的方法,这种方法不需要事先进行大 量的爆破震动数值测试,在仅知道岩石参数和装药 参数的条件下即可对一定爆破规模下某一特定距离 处的爆破震动强度进行估计。在本文中,主要对两 种不同间隔装药条件下的爆破震动强度进行了数值 计算,并与相应的试验结果进行了对比分析。
2 爆破近区数值计算
当炸药在岩石中爆炸后,根据距炮孔中心的远 近不同,可把整个岩石区域分为粉碎区、裂隙区和 震动区。而岩石根据在各个区域中的受力不同也表 现出流体性、弹塑性和弹性等不同的力学特性。而 通常需要保护的被保护物距爆源都不是特别近,也就是说大多处于岩石的弹性震动区,所以这样一来 数值模拟的区域必须要跨越几个不同的区域,因此, 在数值计算中要采用同一种岩石模型是不太合适 的,因而在本文中,数值计算分两步进行:首先在 爆源近区,采用 ALE 算法处理近区塑性大变形问 题;其次,提取爆炸弹性空腔半径上的压力数据, 然后在远区做振动模拟,以获得分析数据。因而进 行近区爆炸地震波模拟分析的主要目的,是提取弹 性空腔半径上的压力参数,为下步远场地震波的模 拟做好数据准备。
2.1 计算模型
本文采用 2 号岩石炸药对水与空气两种不同的 间隔装药结构进行模拟。计算域中包含 4 种物质:2 号岩石炸药、岩石、空气、水。通过 ANSYS 前处 理程序生成三维有限元网格模型,3 种物质均用 SOLIOD164 实体单元进行单元划分。用 ALE 算法 进行计算。为了节省机时,便于计算,由于模型轴 对称,取模型的 1/4 进行研究。模型长 500 cm,宽 200 cm,高 1 400 cm。由于装药直径较小,而所关 心的爆破作用范围较大,因此,采用变步长方式进 行网格划分。XOZ 面和 YOZ 面处理成轴对称面,垂 直 Z 轴 14 m,即 Z 轴方向上端面处理成自由面,其 余作无反射处理。整个模型共划分 103 334 个节点, 93 972 个单元。
2.2 材料模型与状态方程
(1 )材料模型 LS-DYNA3D 中有许多材料模型可用于岩石 模型,如几何帽子模型、伪张量材料模型、 Drucher-Prager 模型、弹塑性流体模型等。本文采用 Drucher-Prager 材料模型,根据试验测定结果取岩石 力学参数为:E =48 GPa,ρ =2.878 g/m3 ,µ =0.23, 内摩擦角φ = ° 45 ,内聚力c = 20 MPa。
2 号岩石炸药采用高能炸药燃烧模型,可以被 看作是一种完全弹塑性材料,该材料模型特点是允 许模拟高能炸药的起爆和爆轰过程。取炸药参数 为:ρ =1.0 kg/m3 ,爆速V = 3 600 m/s,爆压 Pc j − = 3.24 GPa。
(2)状态方程 由于在爆炸场的数值模拟中,炸药的爆轰产物 的压力波动范围很大,从几十万个大气压到低于一 个大气压,很难找到一个适合所有范围的状态方程。 JWL 状态方程能精确描述凝聚炸药圆桶实验过程, 且具有明确的物理意义,因而在爆炸数值模拟中得 到了广泛应用。对高能炸药的爆轰产物采用 JWL 状态方程[4],其一般形式为:
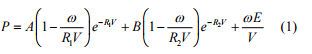
式中A、B、R1、R2 、 ω 为炸药特性参数;P 为压力;V 分别表示爆轰产物的内能和相对体积。对于 2 号岩 石炸药爆轰产物,取 A =214 GPa,B =0.182 GPa, 1 R = 4.15, 2 R = 0.95,ω = 0.3。
对于空气,近似采用理想气体状态方程。
2.3 计算结果
从计算结果可以看出,空气间隔有一个比较明 显的膨胀和衰减过程,水间隔却比较缓慢;同时, 在两种情况下,岩石均受到强烈的冲击压缩,并以 球对称形式向外扩展。
考察空气和水间隔距爆心由近及远单元的应力 变化情况,可知在同等距离处水间隔产生的应力值 比空气间隔大;同时随比例距离的增大,二者的峰 值应力均按幂指数规律逐渐衰减。
3 爆破远区地震波模拟及结果分析
3.1 数值计算模型
模型长 200 m,宽 4 m,高 14 m,为了节省机 时,取 1/2 模型进行研究。计算域包含一种物质: 岩石。共划分 46 900 个节点,38 448 个单元。YOZ 面加冲击载荷,其余除平行于 XOY 面,即 Z 轴上端 面为自由面外,其余为非反射。
3.2 材料模型
由于是考察的远端地震波传播特性,属于弹性 范围,因而岩石材料模型采用弹性材料模型,取暗 色辉长岩,参数如下:ρ =2.878 g/m3 ,E = 48 GPa, µ =0.23。
3.3 加载曲线
本步是爆破震动速度计算的核心部分,前步的 计算只是为该步计算提供计算压力参数。关于压力 的施加主要有两个方面的问题:一是提取压力的位 置,根据本文的计算目的和本步的计算模型,压力 应施加在爆破后岩石的弹塑性分界面上,根据文献[5] 可知,在本文中取 k =4,炸药量 Q=176 kg,可得岩 石的弹塑性分界面距炮孔中心的距离为 2.24 m。即 需要在距炮孔中心 2.24 m 处提取压力曲线,作为本 步中计算的初始输入压力;二是沿 Z 轴方向上压力 提取的位置,由于在本文中炮孔很深,所以在同一 X 轴的截面上,其压力曲线也不尽相同,所以为了 更好地反映真实情况,将加载面沿 Z 轴均匀分割成 两部分,每一部分提取相应的压力曲线,作为此面 上的受冲击应力。按照上述方法提取压力参数,典 型的压力曲线如图 1 所示。
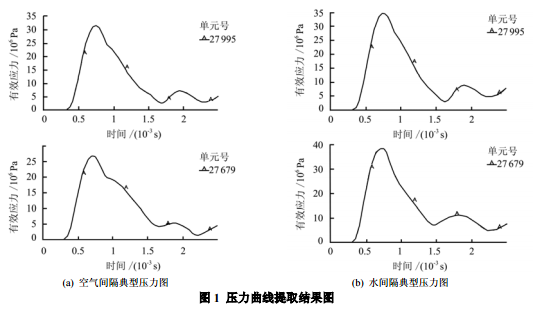
3.4 计算结果与实验对比分析
根据以上的计算模型及参数,对距爆破中心不 同距离的自由面处提取质点垂直震动速度,典型震 速图如图 2 所示。
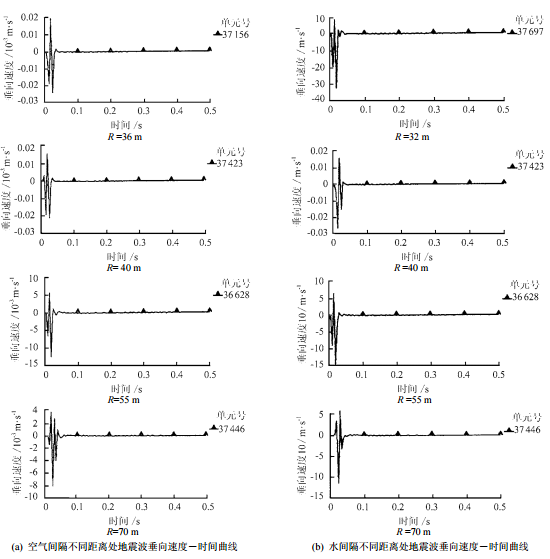
图2 两种情况下不同距离处地震波垂向速度-时间图
然后提取两个模拟结果中的不同质点处的峰值 速度,并与试验结果进行对比,列于表 1。
表 1 两种情况下数值模拟结果与实测结果对
| 测点 | 水间隔装药 | 空气间隔装药 | ||||
| 爆心距 /m | 计算振速 /cm·s-1 | 实测振速 /cm·s-1 | 爆心距 /m | 计算振速 /cm·s-1 | 实测振速 /cm·s-1 | |
| 1 2 3 4 5 6 7 |
36 40 44 59 74 89 104 |
3.22 2.70 2.62 1.48 1.20 0.80 0.65 |
2.87 2.69 2.50 2.40 1,80 1.20 0.94 |
32 36 40 55 70 85 100 |
2.45 2.3 2.10 1.25 0.81 0.72 0.60 |
2.41 2.33 2.19 1.82 1.41 0.92 0.70 |
4 结 语
通过本文中的数值模拟结果可以看出,数值模 拟方法在爆破震动强度预测中是可行而且非常有效 的,特别是其在不需要依赖以往震动测试数据的基 础上就可以对爆破震动强度作出一个比较切合实际 的估计结果,这一点对爆破设计和施工是非常有指 导意义的,同时这也是对现有爆破震动强度预测方 法的一个有益的补充,也为该课题的研究提供了一 条新的途径。

 您现在的位置:
您现在的位置: